 |
Fast, robust, planar swept volumes
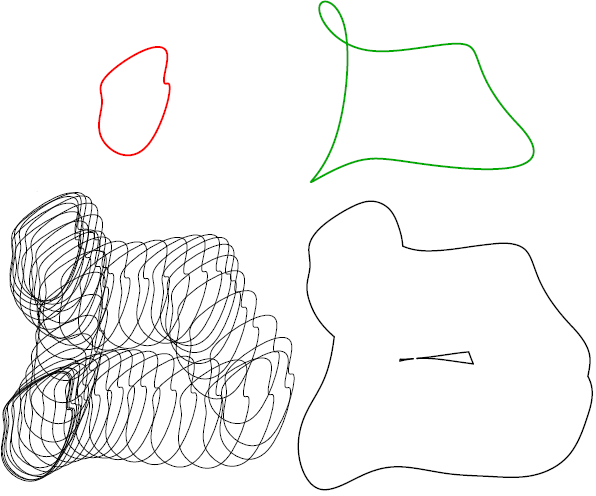
Sweeping is one of the fundamental shape descriptors in solid modeling. While some of the underlying theory was recently uncovered, the question of writing a numerically robust implementation remained wide open, for the 3D as well as the 2D case. This effort aims to address this question for the 2D case. Handling global self-intersections in the envelope in a numerically stable as well as fast manner has been the special focus of this work. But enough of words. The proof of the pudding lies in the eating and you are invited to feast your eyes on the 15K examples, along with animations, generated from a C++ based implementation of the algorithm. See the 15K Table. Read more. |
|
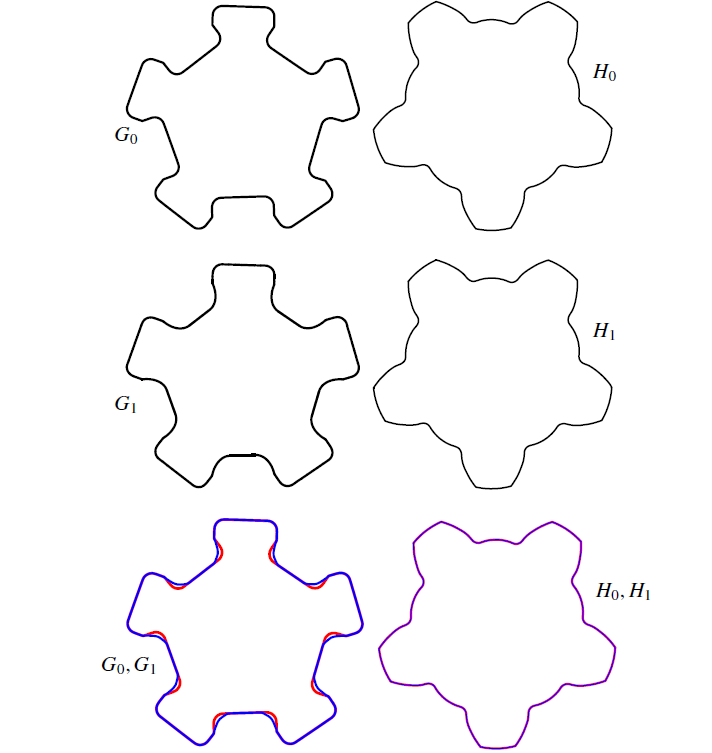
Conjugate shape simplification and planar gear design
This work proposes an algorithm to simplify the shapes of planar gears. This is achieved via iterative conjugation, using precise algebraic sweeps. The notion of shape simplification is introduced in a mathematically rigorous manner and it is shown that the conjugation process converges, yielding a pair of meshing gears that follow the desired motion. Simplified gear shapes may lead to improved mechanical characteristics and reduction in manufacturing costs. The generality of algebraic sweeps allows precise design of gears with freeform shapes and non-uniform motion transmission. With Henry Segerman and Gershon Elber. Read more. Watch demo. |
 |
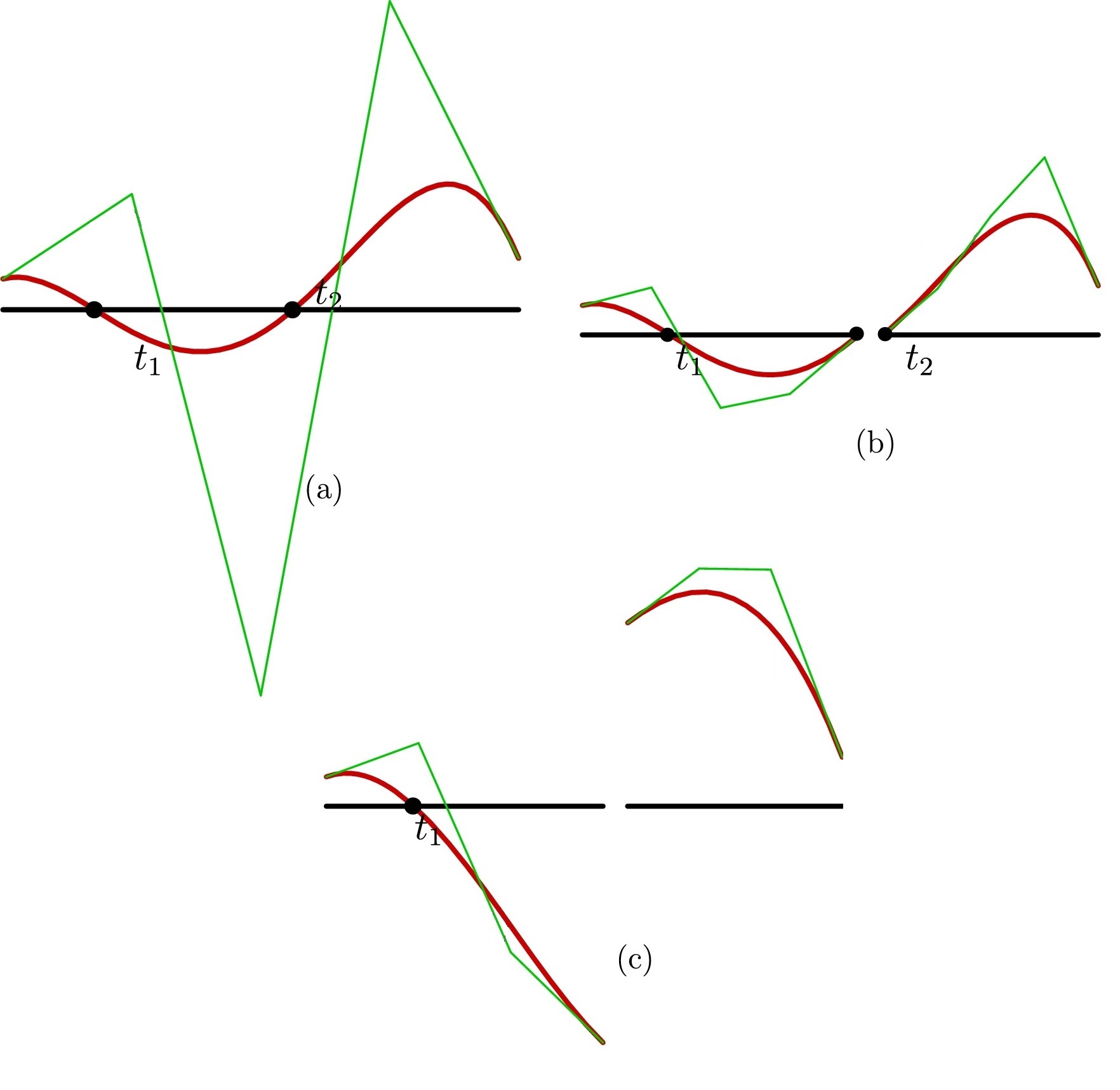 |
Zeros of univariate scalar Bernstein polynomials
In Machchhar and Elber (2016), an algorithm is presented for computing all real roots of univariate scalar Bernstein polynomials by subdividing the polynomial at a known root and then factoring out the root from the polynomial, resulting in a reduction in problem complexity. This short report presents a speed-up over Machchhar and Elber (2016), by circumventing the need for subdividing the polynomial each time a root is discovered, an O(n) process, where n is the order of the polynomial. The subdivision step is substituted for by a polynomial division. With Gershon Elber. Read more. |
|
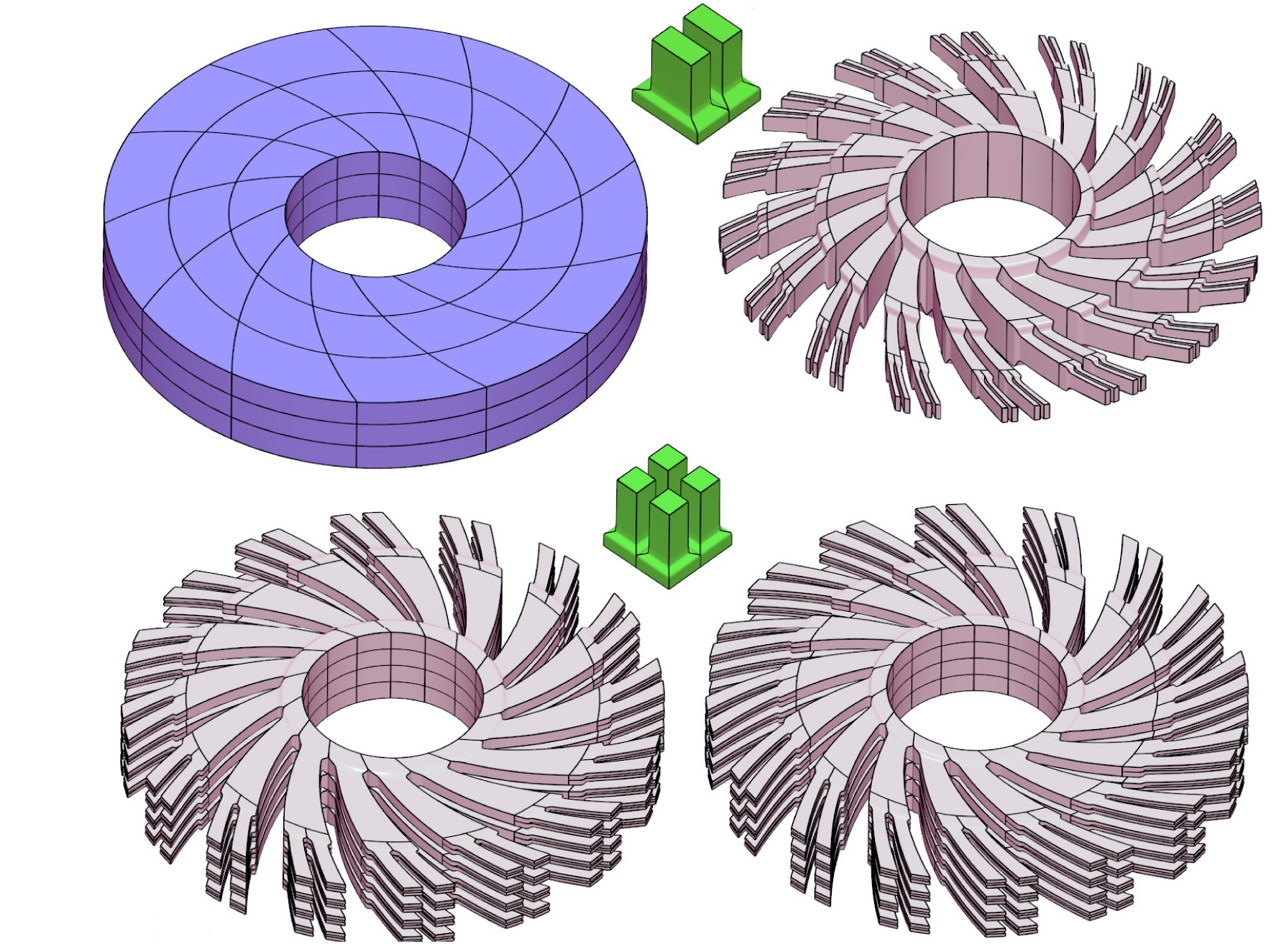
Hierarchical micro-structures via functional composition
This work proposes new methods and algorithms for the construction of micro-structures that leads to a high degree of precision and water-tight models. That proposed approach involves the tiling of the domain of a deformation map using copies of a tile. The resulting tiling is functionally composed into the deformation map to obtain freeform micro-structures. Such a decoupling of the micro and macro structures allows a simplified control over design parameters. Herein, we present several extensions to this micro-structure construction scheme, comprising bivariate and trivariate tiles, implicit and parametric, including with potential discontinuities. With Fady Massarwi, Pablo Antolin and Gershon Elber. Read more. |
 |
 |
CNC machining simulation
This work presents an algebraic based approach and a computational framework for the simulation of multi-axis CNC machining of general freeform tools. The boundary of the swept volume of the tool is precisely modeled by a system of algebraic constraints, using B-spline basis functions. Subdivision-based solvers are then employed to solve these equations, resulting in a topologically guaranteed construction of the swept volume. The presented algebraic-based method readily generalizes to accept tools of arbitrary free-form shape as input, and at the same time, delivers high degree of precision. Being a common representation in CNC simulations, the computed swept volume can be reduced to a dexels’ representation. With Denys Plakhotnik and Gershon Elber. Read more. |
|
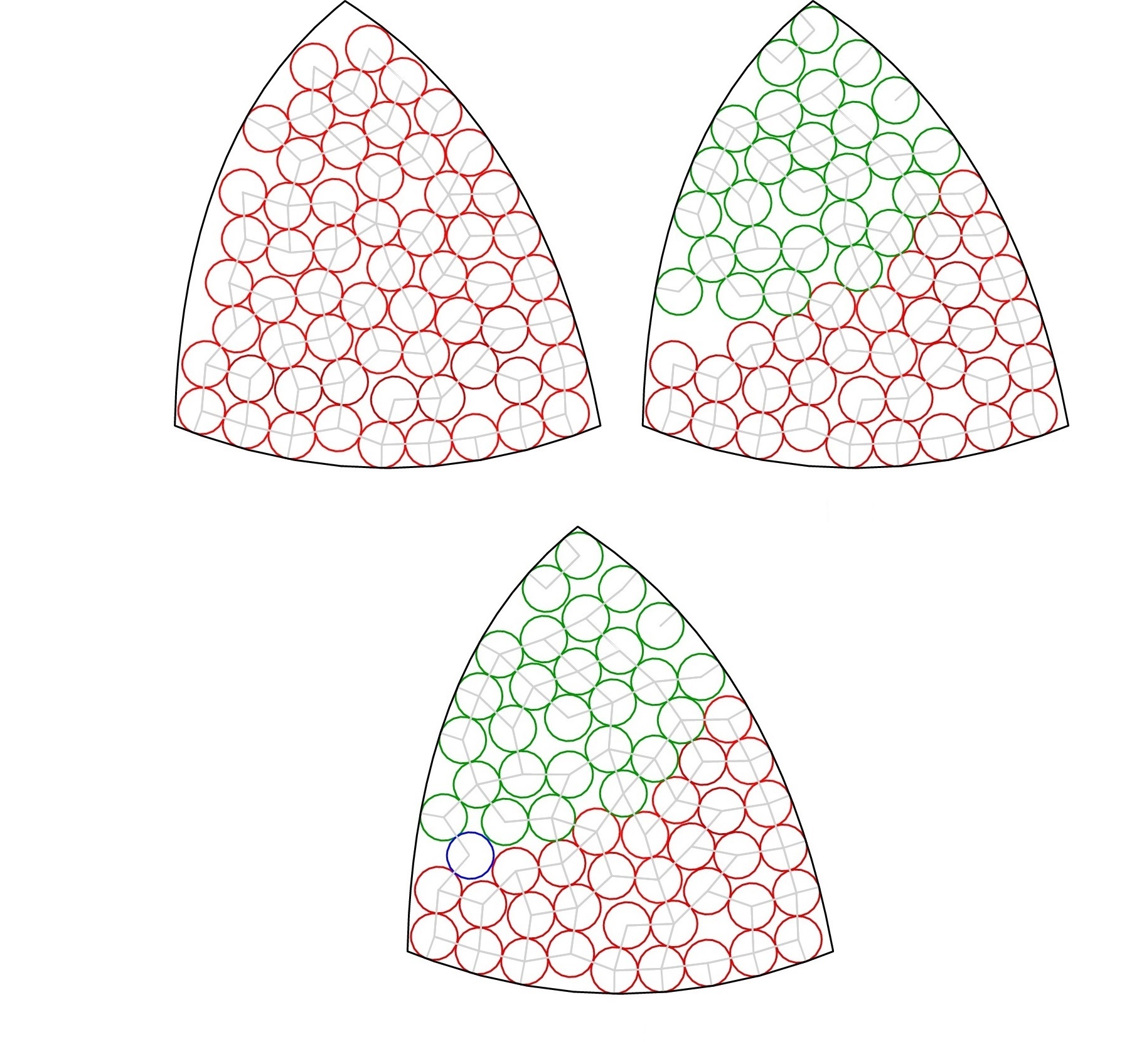
Circle packing in freeform containters
This work proposes an algorithm for computing dense packings of congruent circles inside general 2D containers. Unlike the previous approaches which accept as containers, only simple, symmetric shapes such as circles, rectangles and triangles, our method works for any container with a general, freeform (spline) boundary. In contrast to most previous approaches which cast the problem into a non-convex optimization problem, our method attempts to maximize the number of packed circles via a perturbation approach and consists of two main phases. In the first phase, an initial packing is computed by placing circles in spiraling layers, starting along the boundary of the container. The next phase simulates the shaking of a container under gravity, thereby making room for additional circles by perturbing the existing circles. With Gershon Elber. Read more. |
 |
 |
Covering 2D domains with random curves
This work considers the problem of covering a given 2D convex domain D with a C1 random-looking curve C. C within D is said to cover D up to ϵ > 0 if all points of D are within ϵ distance of C. This problem has applications, for example, in manufacturing, 3D printing, automated spray-painting, polishing, and also in devising a (pseudo) random patrol-path that will visit (i.e. cover) all of D using a sensor of ϵ distance span. Our distance bound approach enumerates the complete set of local distance extrema, enumeration that is used to provide a tight bound on the covering distance. With Gershon Elber. Read more. |
|
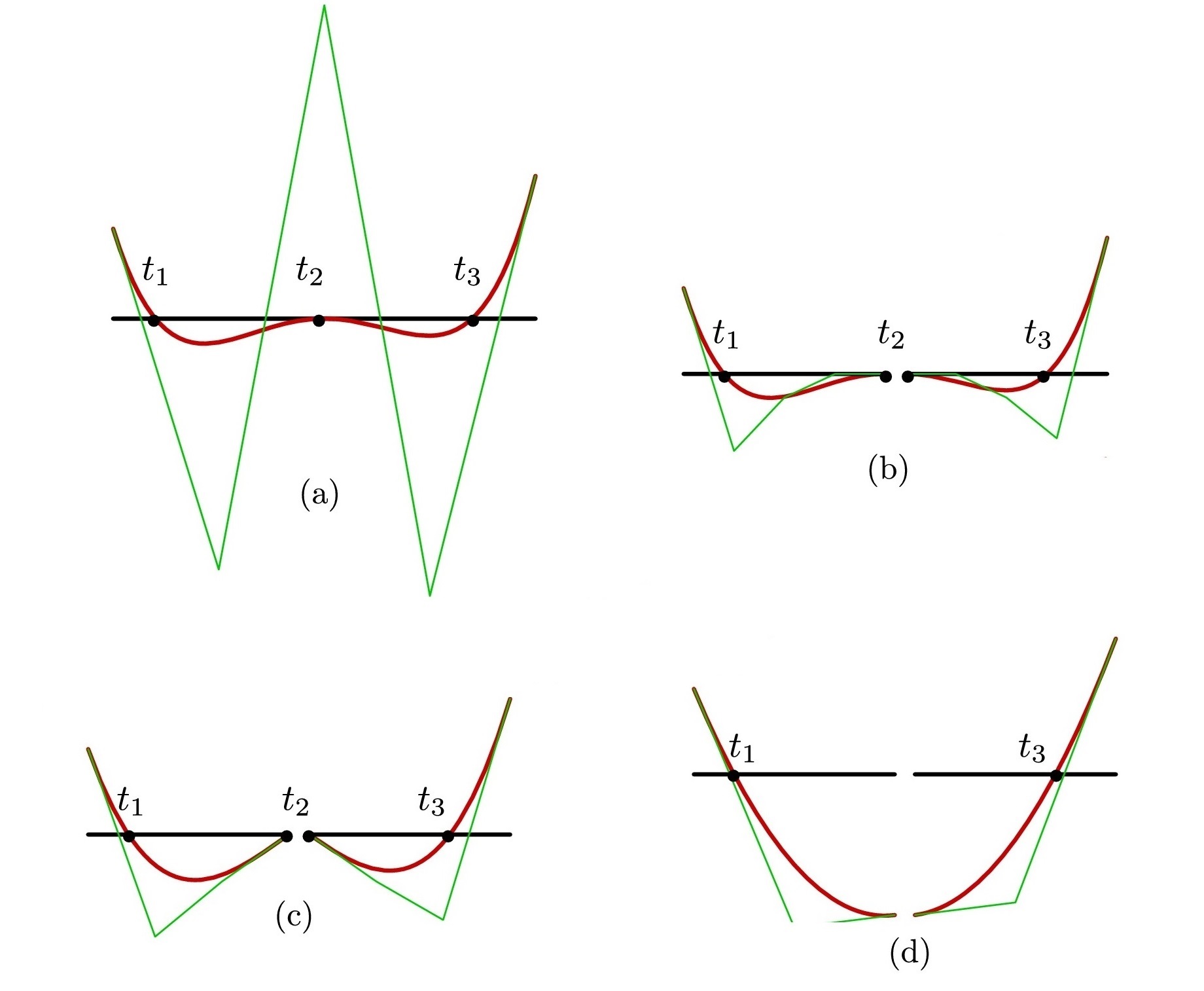
Zeros of Univariate Scalar Beziers
This work proposes a fast algorithm for computing the real roots of univariate polynomials given in the Bernstein basis. Traditionally, the polynomial is subdivided until a root can be isolated. In contrast, herein we aim to find a root only to subdivide the polynomial at the root. Comparison of running times against the state-of-the-art on thousands of polynomials shows an improvement of about an order-of-magnitude. With Gershon Elber. Read more. |
 |
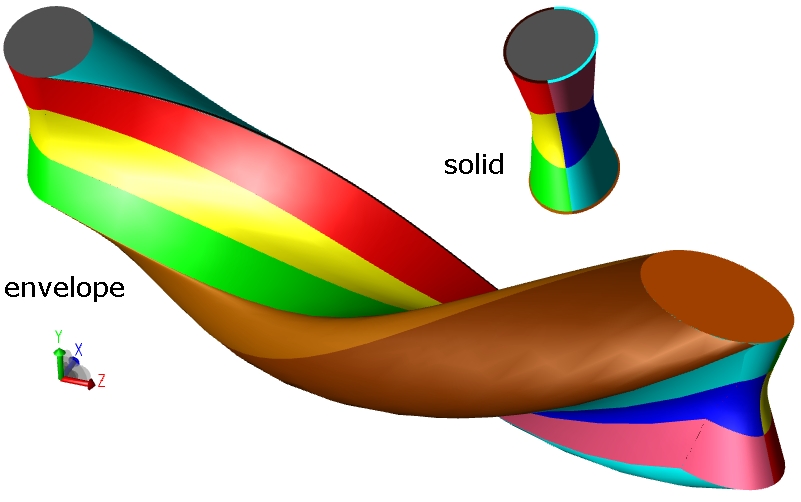 |
Incorporating sharp features in soild sweeps
This work extends the computational framework for solid sweeps to handle input solids with G1 discontinuities. Unlike in the smooth case, a sharp point on the solid boundary has a cone of outward normals. The interplay between this cone of normals at a sharp point on the solid and the trajectory leads to efficient computational constructs for computing the parts of the envelope generated by sharp features. We also show that the parts of the envelope generated by sharp features are free of local self-intersections. With Bharat Adsul and Milind Sohoni. Read more. |
|
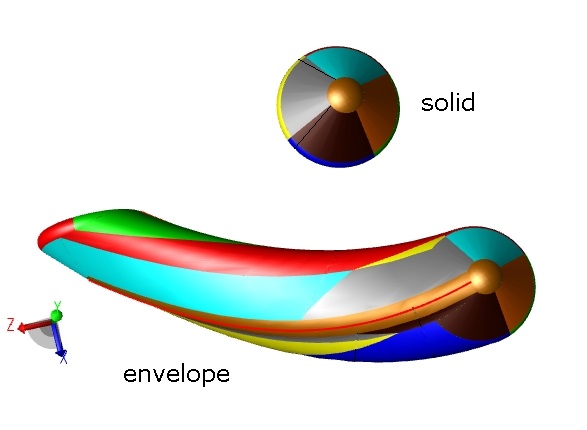
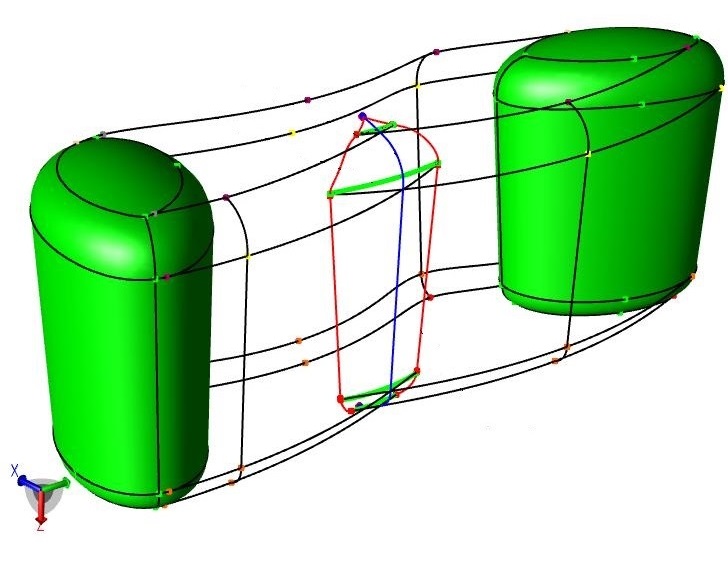
A computational framework for solid sweeps
The boundary representation, or brep, is a de facto standard for the computer representation of 3D solids in CAD. This work addresses the issues involved in computing the brep of the swept volume, namely, the adjacency relations amongst the faces, edges and vertices of the envelope and their orientations. The brep structure of the envelope is derived from that of the solid via the natural correspondence between the two which is illustrated by color coding in the adjacent figure. This correspondence is illustrated in the example via color-coding. With Bharat Adsul and Milind Sohoni. Read more. |
 |
 |
Solid sweeps: Local and global analysis
Solid sweep involves computing the infinite union of all the transforms of a given solid moving along a given one parameter family of rigid motions. This work performs a delicate analysis of the local and global self-intersections in the envelope. A novel geometric invariant is proposed which aids in identifying and resolving singularities and self-intersections. Also, a procedural parameterization of the envelope surface is given, with time as one of the parameters. With Bharat Adsul and Milind Sohoni. Read more. |